Remake | CS50 AI入门笔记

Introduction to AI

术语

1. actions

   在某一状态下可以作出的选择

   ACTION(s) 返回在状态s下可以采取的行动集合。

2. transition model

   针对某个状态采取某个动作后产生的结果

   RESULT(s, action)返回由当前状态采取某行动后生成的新模型。

3. state space

   从初始状态开始经过一系列行为可能产生的状态。

Search

search problems contain

1. initial state
2. actions
3. transition model
4. goal test 测试给定的状态是否为目标状态
5. path cost function 代价计算

Node

是一种记录当前状态信息的数据结构，其中包含：

1. 当前状态描述
2. 父状态
3. 由父状态转移到当前状态采取的行动
4. 到达当前状态的消耗

MiniMax

进行二元博弈时，做最坏的打算，尽最大的努力。

博弈结果用分数来表示，A胜加分，B胜减分。一方尽可能的使分数增大，一方尽可能的使分数减少。

由于任何一方在做决策时都会受到另一方之前所作决策的影响。例如A要在B尽可能降低了分数的情况下，作出最大程度提高分数的决策。

def MAX_VALUE(state):
    # 若当前状态对局已结束，则返回对局结果
    if TERMINAL(state):
        return UTILITY(state)
    # 初始化当前分数为负无穷
    v = -INFINITY
    # 尝试所有可以由当前状态派生出的状态，计算对手在派生状态中采取的降低分数的决策。选取所有派生中仍旧能带来最大收益的状态。
    for action in ACTIONS(state):
        v = MAX(v, MIN_VALUE(RESULT(state, action)))
    return v

如此递归的求解可能的状态，效率并不高，因此可以做一定的剪枝操作，例如当派生状态1的最小收益为4时，若派生状态2已经确定其最小值小于4（孙子状态有收益值已经小于4了，则对手采取操作后该派生的最大收益必定不可能大于4）。此时可以直接忽略该状态。

Limit Minimax

限制minimax的求解次数，例如限制搜索树的深度，每一步决策只尝试计算之后X步的可能状态。同时添加一个估计函数，判断达成目标的可能性。

Knowledge

model:负责对所有可能的逻辑语句作出判断

knowledge base: 计算机初始情况下已知正误的逻辑语句集合

model check：依据已有的知识来推断给定的语句是否成立。罗列所有的可能性，判断何时前置条件与查询结果均成立。

def model_check(knowledge, qeury):
    
    def check_all(knowledge, query, symbols, model):
        # all of the symbols have been assigned
        if not symbols:
            # if this model is compatiable with knowledge
            # return whether query is compatiable with model
            if knowledge.evaluate(model):
                return query.evaluate(model)
            # else this model is nonsense to us
            return True
        else:
            remaining = symbols.copy()
            # pop a symbol to assign
            p = remaining.pop()
            # 分两种情况讨论，当前条件为真或当前条件为假
            model_true = model.copy()
            model_true[p] = True
            model_false = model.copy()
            model_false[p] = False
            # 如果两种情况无法同时为真，就代表还有其他条件影响结果，此时不能得出结论。但若同时为真，就代表无论其余条件是什么，目前已有知识已经足够作出判断
            return check_all(knowledge, query, remaining, model_true) && chekc_all(knowledge, query, remaining, model_false)
    
    symbols = set.union(knowledge, query)
    check_all(knowledge, query, symbols, dict())

Probability

unconditional probability

在没有任何前提条件的情况下作出判断

conditional probability

基于某些前提，判断某件事发生的可能性。

符号表示P(a | b)，在b发生的前提下，a发生的可能性。

random variable

象征所有可能出现的情况。

independence

某事件的发生不会影响其他事件发生的可能性。

即某两个事件相互之间没有关联。

贝叶斯公式

P(b | a) = P(a | b) * P(b) / P(a)

可以通过该公式，可以推算出一些难以观测的情况的发生概率

已知在某未知原因下某件有明显影响事件的发生概率，就可以推算出在该明显影响下，对应的未知原因发生的概率。

例如，每一份疾病报告的正确性难以观测，但在疾病发生的前提下，对应报告的正确率容易采集，这样就可以推算出一份报告检测出疾病的概率。

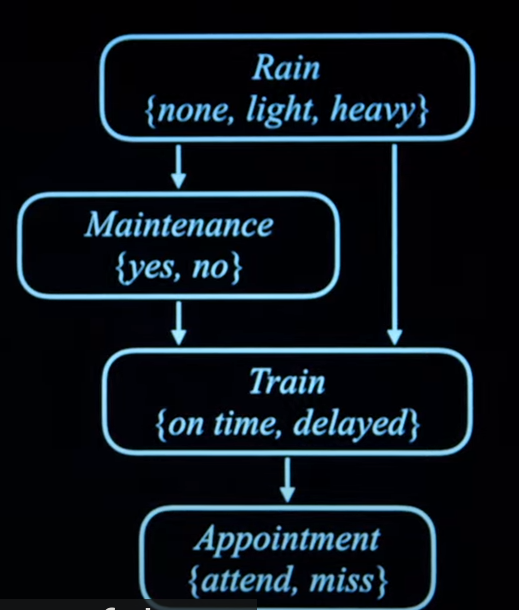
贝叶斯网络

用于表示random variables之间依赖关系的数据结构。

结构

1. 有向图

2. 每一个节点象征一个随即变量

3. 从X指向Y的箭头表示X是Y的父节点

4. 每一个节点都有可能性分布 P(X | Parent(X))

   

推论操作

1. 枚举

• Query X：需要计算概率分布的变量
• Evidence variables E：已知的事件e的变量
• Hidden variable Y：不是以上二者的变量

$$
P(X|e) = αP(X,e)=α\sum_yP(X,e,y)
$$

2. 样本

   生成一定数量的样本，在样本中筛选出符合条件的样本用于计算概率。

   例如，若要求推断火车准点的概率，则查看火车准点在样本中的占比。若有前提条件，则先筛选出满足前提的样本，然后根据这些样本推断概率。

   优化：由于样本生成没有规律，若某个前提条件发生的可能性很小，那么就会导致大量的算力被浪费在生成无用的样本上。

   此时可以采取可能性加权的方式进行优化。

   在获取样本时，固定前提条件必然满足，之后计算在该样本的所有前置条件中，要求的前提条件满足的可能性，可能性越高，权重越大。

   例如：前提条件是火车准点，则在生成一个样本后，根据样本中的天气情况以及道路维护状态计算火车准点的可能性，依此为样本赋予权重。

Markov model

用于模拟伪随机变化系统的随即模型，假设当前的状态只与依赖有限的过去的状态。

Markov chain

一个随机变量序列，其中每一个变量的分布都遵循Markov假设。

Hidden Markov model

也是一条Markov链，但其中的状态很难被直接且准确地观测到。但一些可观测到的事件可以帮助推断出隐藏的状况。例如：街上的人都带着雨伞 -> 今天下雨。

Task	Definition
filtering	根据目前已知的观测结果，计算当前状况的概率分布。
prediction	根据目前已知的观测结果，计算未来状况的概率分布。
smoothing	根据目前已知的观测结果，计算过去状况的概率分布。
most likely explanation	根据目前已知的观测结果，计算最可能的状态序列。